군집 알고리즘은 대표적인 비지도 학습 중의 하나이다. 비지도 학습은 해석하기가 어렵지만, 방대한 데이터를 탐색할 때 좋은 방법 중의 하나이다. 특히, 데이터가 적고 feature가 많은 경우에 과적합을 방지하는데 도움이 되기도 한다. 가장 많이 회자되는 군집 알고리즘은 K-mean 군집 알고리즘이 아닐까 한다. 오늘은 이와는 좀 다른 SOM 군집 알고리즘에 대해서 알아보도록 하겠다.

SOM군집 알고리즘은 데이터의 분포를 고려해서 클러스트링할 수 있는 알고리즘이다.
k-means알고리즘은 가까운 거리에 있는 데이터를 하나의 군집으로 묶는다. 그래서 다른 분포의 데이터가 섞여 있는 경우에 잘못 군집화가 될 수 있다. 이를 해결하기 위해 데이터의 분포를 기반으로 군집화할 수 있는 알고리즘을 사용한다.
가장 대표적으로는 DBSCAN(density-based spatial clustering of application with noise) 알고리즘이 있다. 이 알고리즘은 거리와 군집화할 최소 샘플수를 지정해야 한다.
무작위로 포인트를 선택한 후에 주어진 거리 안에 최소 샘플수 이상의 포인트가 있으면 군집화를 한다. 최소 샘플수보다 적다면 이 데이터들은 어디에도 속하지 않는 잡음(noise)로 분류한다. 새로 군집에 포함된 데이터도 같은 방식으로 군집화할 수 있는 데이터를 찾는다.
SOM은 저차원(2차원 또는 3차원)의 공간에 데이터를 차원 축소하여 군집화하는 알고리즘이다.
이 저차원의 공간을 '경쟁층'이라고 부른다. 첫 번째 데이터가 들어오면 경쟁층의 어떤 노드와 가장 가까운 지 계산하고, 해당 노드에 할당합니다. 이를 winning node라고 합니다.
그리고, winning node외의 다른 노드들을 입력 데이터를 기준으로 학습(가중치 조정)시킨다. 자세한 설명은 아래 포스팅을 참조하는 것이 도움이 될 듯 하다.
[머신러닝] - 자기조직화지도(Self-Organizing Map, SOM)
1. 개요 대뇌피질의 시각피질의 학습 과정을 모델화한 인공신경망으로써 자율 학습에 의한 클러스터링을 수행하는 알고리즘이다. 2. 용어 정의 클러스터링(clustering): 데이터의 유사성에 기초하
untitledtblog.tistory.com
자기조직화지도(Self-Organizing Map) · ratsgo's blog
이번 글에서는 차원축소(dimensionality reduction)와 군집화(clustering)를 동시에 수행하는 기법인 자기조직화지도(Self-Organizing Map, SOM)를 살펴보도록 하겠습니다. 이번 글 역시 고려대 강필성 교수님 강
ratsgo.github.io
필자가 이해한 바로는 입력 데이터를 2차원의 노드 중에 가장 가까운 노드에 할당하고 나면, 나머지 노드들은 입력 데이터를 반영하여 할당된 노드와 거리가 더 멀이지게 학습하는 듯 하다.
이렇게 할당된 2차원의 공간을 클러스트링을 하여 군집을 만든다.
SOM알고리즘을 이야기하면서 가장 많이 보는 것 중의 하나가 2차원의 공간을 시각화한 모습이다.
각 노드에 해당하는 입력 데이터의 값을 표현함으로 어떤 특성의 데이터들이 군집화되었는지 추측해볼 수 있다.

k-means알고리즘과 som알고리즘을 적용하여 비교해보았다. 파이썬에서 som알고리즘을 적용하는 패키지는 여러 개 있겠지만, 필자는 som-learn이라는 패키지를 이용하였다.
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn as sk
import sklearn.cluster as cluster
x=np.random.randn(10000)
y=np.random.randn(10000)
df=pd.DataFrame({"x":x,"y":y})
df["dis"]=df["x"]**2+df["y"]**2
df["cla"]=df["dis"].apply(lambda x:1 if 0.5<x<1.0 else 2 if 3<x<4 else 0)
df["cla"].value_counts()
df=df[df["cla"]!=0]
sns.scatterplot(df["x"],df["y"],hue=df["cla"])
아래와 같은 형태의 데이터를 만들었다.

k-means알고리즘을 적용해 보았다.
model=cluster.KMeans(2)
model.fit(df[["x","y"]])
df["pre"]=model.predict(df[["x","y"]])
sns.scatterplot(df["x"],df["y"],hue=df["pre"])

som 알고리즘을 적용해보았다.
from somlearn import SOM
CLUSTERER = SOM(n_columns=1, n_rows=2, gridtype='hexagonal', random_state=70)
y_pred = CLUSTERER.fit_predict(df)
df["pred"]=y_pred
sns.scatterplot(df["x"],df["y"],hue=df["pred"])
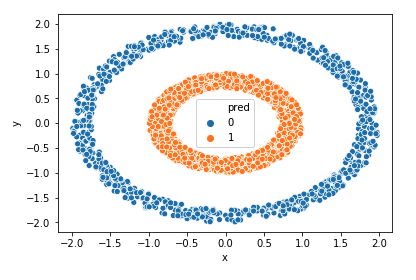
오늘은 이렇게 SOM알고리즘에 대해서 알아보았다. 분포를 고려해서 군집화하고 시각화를 통해 군집에 대한 성격을 알아볼 수 있어 유용하지 않을까 싶다.
'데이터 > 데이터 분석' 카테고리의 다른 글
| 추천 알고리즘 탐색, Factorization Machine 알아보기 (0) | 2022.01.18 |
|---|---|
| 범주형 데이터 기준 의사결정나무 알고리즘 만들기 (0) | 2022.01.17 |
| 데이터 분석 용어 정리 - Funnel, adhoc 분석 (0) | 2022.01.17 |
| XGBoost와 랜덤 포레스트 재학습 하는 방법은? (0) | 2022.01.17 |
| 파이썬 판다스 데이터프레임 리스트로 추출하는 방법은?! (0) | 2022.01.15 |
| 파이썬 A/B테스트 필요샘플 크기 확인 법, 검정력 테스트?! (0) | 2022.01.15 |
| 지역별(시군구, 동단위까지) 소득 통계 데이터 수집하는 3가지 방법 (2) | 2022.01.14 |
| 파이썬 A/B 테스트 하는 방법은?! (0) | 2022.01.14 |



